Co-ordinate System
A coordinate system is a
way of uniquely expressing the location of a point (or other geometric
object) on a manifold - for example, Euclidean space. So
if you want to describe where something is then you need
a coordinate system.

1. Rectangle Co-ordinate System : -

1. Rectangle Co-ordinate System : -
The most common coordinate system for
representing position in space is one based on three perpendicular
spatial axes generally designated x, y, and z.
Any
point P may be represented by three signed numbers, usually written (x, y, z)
where the coordinate is the perpendicular distance from the plane formed by the
other two axes.
Often positions are specified
by a position vector r which can be expressed in terms of the coordinate values
and associated unit vectors.
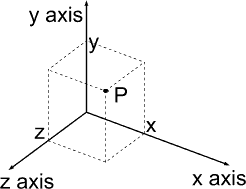
[Figure-1.1 Rectangular coordinate system]
Cartesian to Cylindrical Coordinate Transformation:-
The images shown below are of rectangular co-ordinate system:-
2. Cylindrical Co-ordinate System : -
[Figure-1.2 Cylindrical coordinate system]
The cylindrical coordinate system basically is a combination of the polar coordinate system xy plane with an additional z ¡coordinate vertically. In the cylindrical coordinate system, a point P (x,y,z); whose Cartesian coordinate is (x,y,z); is assigned by the ordered triple (r,z); where (r) is the polar coordinate of (x,y) the vertical projection along z¡axis of P onto xy plane.
Cylindrical to Cartesian Coordinate Transformation:-
The images shown below are of cylindrical co-ordinate system:-

3. Spherical Co-ordinate System : -
[Figure-1.3 Spherical coordinate system]
Spherical coordinates are
another generalization of 2-D polar coordinates. However, in this coordinate
system, there are two angles, theta and phi.
Let's consider a point P that is specified by
coordinates (x,y,z) in
a 3-D Cartesian coordinate system. The same point can be represented in
spherical coordinates as (r,theta,phi,) where r, theta,
and phi are functionally related
to x, y,
and z.
Spherical to Cartesian Coordinate Transformation:-
X=r
sin θ cos
Φ,
Y=r
sin θ sin Φ,
Z=z
cos θ
The images shown below are of spherical co-ordinate system:-
Links of the quiz are given below:
1) https://docs.google.com/forms/d/e/1FAIpQLSdIuRAa0Ihgy42avk4UY5pFno42vEm1Km5dlU8MIzLLvrqHLA/viewform?usp=sf_link
2) https://docs.google.com/forms/d/e/1FAIpQLSfzIVylWi77citu-yCZFuH8qFIHTO0ZQns3qOIQ3vdhGz2gwQ/viewform?usp=sf_link













